Tipos de funciones (https://www.lifeder.com/tipos-de-funciones/)
Tipos de funciones y sus gráficas
Existen diversos tipos de funciones que se utilizan para modelar problemas en ramas del saber como ciencias naturales, administración, economía y ciencias sociales. Matemáticamente hablando, una función es una relación entre dos o más variables
Las variables suelen llamarse con las letras x e y, con x como la variable independiente e y como la variable dependiente. Naturalmente pueden llamarse de cualquier otro modo, eligiendo el nombre de la variable en concordancia con la magnitud que representa.
- f (x) = x + 1
- La población P de cierta ciudad en cierto intervalo de tiempo t.
- h(x) = {(1,3); (2,4); (3,5); (4,6)}
Clasificación de las funciones
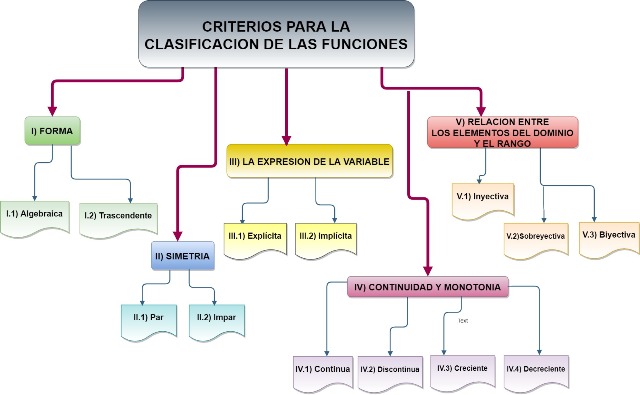
Las funciones pueden agruparse en 5 grandes categorías, tal como se refleja en el siguiente esquema, en el cual cada grupo se etiqueta con un número romano y un color. Comenzando de izquierda a derecha, las funciones se clasifican de acuerdo a:
- I) Su forma.
- II) La simetría.
- III) La manera de expresar la variable.
- IV) Su continuidad y monotonía.
- V) La forma en que se relacionan los elementos del dominio con los del rango.
Ahora sigue una breve descripción de cada uno de los tipos de funciones con sus respectivos ejemplos.
I) Funciones según su forma
I.1) Funciones algebraicas
Se encuentran entre las funciones más utilizadas en numerosos campos de la ciencia, y por ello son de las más conocidas. Se caracterizan por tener como regla de correspondencia, una expresión algebraica.
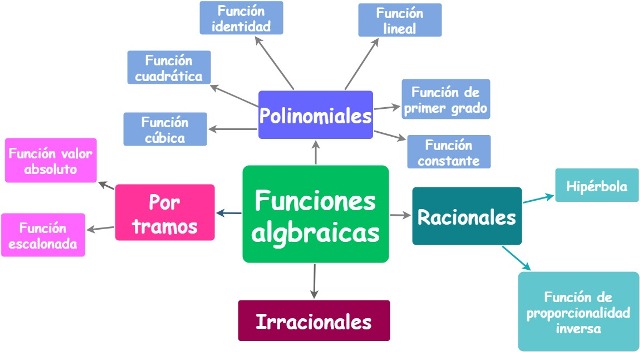
A su vez, las funciones algebraicas se subdividen en los siguientes tipos:
- I.1.a) Polinomiales o polinómicas.
- I.1.b) Racionales.
- I.1.c) Irracionales.
- I.1.d) Por tramos.
I.1.a) Funciones polinomiales o polinómicas
Consisten en sumas de términos cuya forma general es:
P(x) = anxn + a n-1xn-1 +…a1x + a0
Donde los coeficientes an, a n-1… a1, a0 son números reales y n es un número entero. El dominio de las funciones polinomiales es el conjunto R de los números reales y además son funciones continuas a lo largo de dicho dominio.
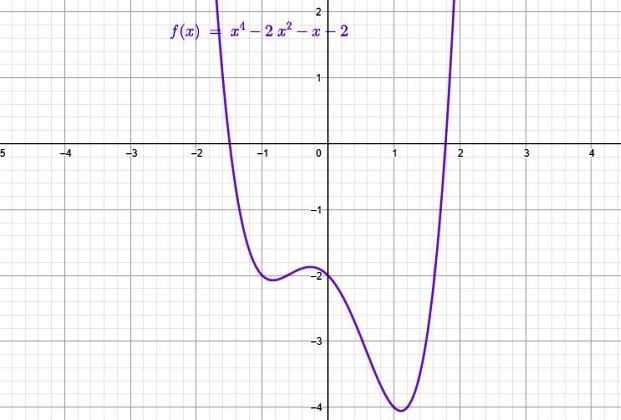
En la figura superior está la gráfica de la siguiente función polinomial de orden 4:
f(x) = x4 – 2x2 – x -2
Entre las funciones polinomiales se distinguen algunos casos particulares, según los valores de los coeficientes. Vale la pena considerarlas con detenimiento, pues son de gran utilidad en múltiples situaciones:
i) Función constante
Se tiene una función constante cuando todos los coeficientes se anulan, excepto a0:
f(x) = a0 = k
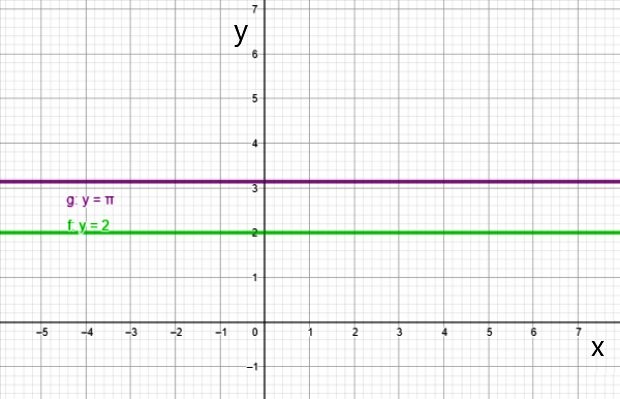
La gráfica de la función constante es una línea recta paralela al eje horizontal, como por ejemplo las rectas:
- f (x) = 2
- g (x) = π
- h (x) = -3/2
ii) Función de primer grado
La función de primer grado o función afín es aquella cuya gráfica es una línea recta. Es un caso particular de la función polinomial donde todos los coeficientes de anulan excepto a1 y a0. Viene dada por:
f (x) = a1x + a0
El valor a1 es la pendiente de la recta, que da una medida de su inclinación, y a0 es el corte de la recta con el eje vertical. Ambos pueden tomar valores positivos o negativos.
Ejemplos de función de primer grado son los siguientes:
- g(x) = 2x -1
- h(x) = -6x +5/2
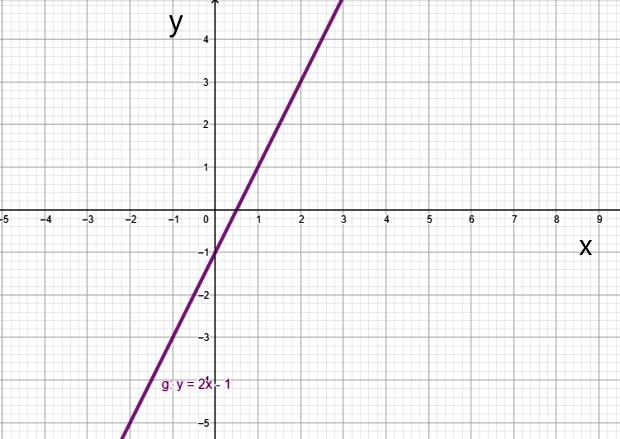
Hay un caso especial, que es la función lineal.
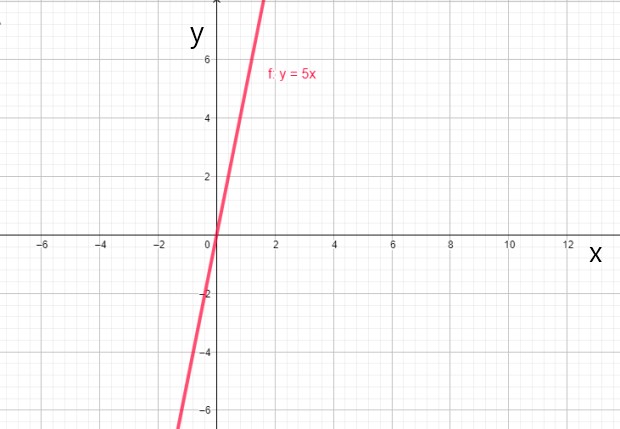
iii) Función lineal
Cuando el coeficiente a0 es 0, la función siempre pasa por el origen y se expresa mediante f (x) = a1x, denominándose función lineal, como estas:
- f(x) = 5x
- g(x) = -7x
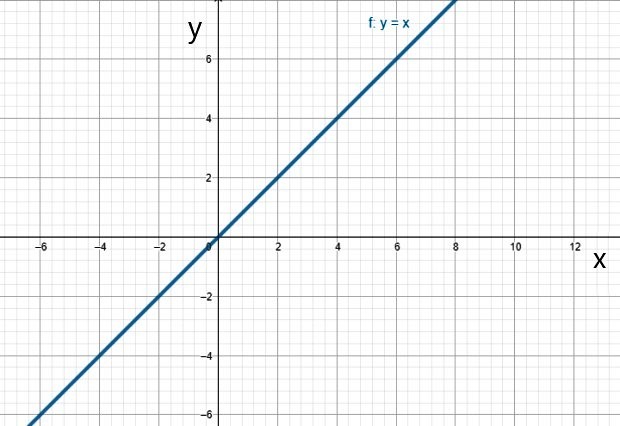
iv) Función identidad
Es un caso particular de la función lineal, en el cual a1 = 1:
f(x) = x
v) Función cuadrática
Tiene la forma general:
f(x) = a2x2 +a1x + a0
Con a2 ≠0.
Su gráfica es una parábola cuyo eje axial o de simetría es paralelo al eje de las ordenadas. Siempre intersecta al eje vertical en el punto de coordenadas x = 0, y = a0. En cuanto a las intersecciones con el eje horizontal, puede tener hasta un máximo de 2.
Ejemplos de funciones cuadráticas son:
- f(x) = x2 – 3x – 4
- g(x) = 4x2
- h(x) = x2-1

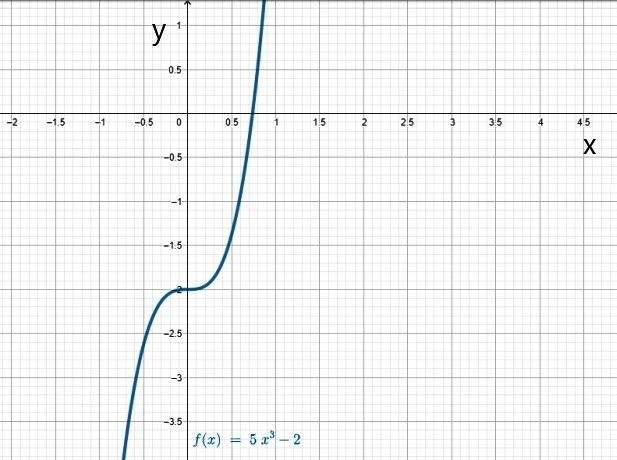
vi) Función cúbica
Como su nombre lo indica, la función cúbica contiene una potencia de 3:
f(x) = a3x3 + a2x2 + a1x + a0
El coeficiente a3 siempre es distinto de 0, como en estos casos:
- f(x) = x3
- g(x) = 5x3 – 2
- h(x) = -3x3 + 4x2 + 10x + 1
I.1.b) Funciones racionales
Las funciones racionales tienen la forma:
Donde P(x) y Q(x) son polinomios irreducibles, es decir, no tienen ningún factor en común y en todo caso Q(x)≠0.
Del dominio de las funciones racionales se excluyen todos los valores que anulan al denominador Q(x), es decir, sus raíces, mientras que del rango se excluyen los valores de y que determinan las asíntotas horizontales.
Una asíntota es una recta a la cual la función se acerca, tanto por la izquierda como por la derecha, por encima o por debajo, pero que jamás cruza. Tales rectas pueden ser verticales, horizontales o inclinadas.
Ejemplos de funciones racionales son:
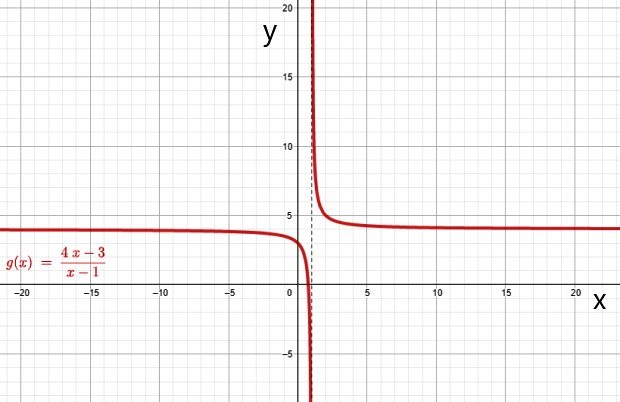
i) Hipérbola
La gráfica de una función racional es una hipérbola cuando el polinomio en el denominador Q(x) tiene grado 1. La gráfica de las funciones f(x) y g(x) de los ejemplos de arriba son hipérbolas, se puede comprobar fácilmente a través de un software de graficación online gratuito, como Geogebra.
ii) Función de proporcionalidad inversa
Es una función de la forma:
Donde c es un número real diferente de 0. Su dominio es el conjunto de los números reales exceptuando el 0.
I.1.c) Funciones irracionales
Son aquellas cuya variable independiente se encuentra bajo un signo radical. Su forma general es:
Algunas de estas funciones pueden ser:
El dominio de estas funciones se determina como sigue:
-Si las raíces son de índice par, la cantidad subradical f(x) siempre debe ser 0 o positiva.
-Cuando las raíces son impares, f(x) puede ser positiva o negativa. Por lo tanto en este caso el dominio de la función son los números reales.
Por ejemplo, el dominio de:
Es el conjunto de los números reales tales que x-3 sea mayor o igual a 0. En tal caso, x debe ser mayor o igual a 3. Por lo tanto el dominio de esta función es el conjunto de valores del intervalo [3,∞+).

I.1.d) Funciones a trozos o por tramos
La función por partes, por tramos o a trozos es aquella que requiere más de una fórmula para distintos valores del dominio. He aquí algunos ejemplos de su aplicación:
-Tarifas para el envío de paquetes por correo, según el peso o el volumen, el origen y el destino de los mismos.
-Tarifas para servicios, por ejemplo telefonía y electricidad.
-Venta de entradas para museos o parques de diversiones, según la edad.
En forma matemática, una función por partes puede ser, por ejemplo:
El dominio de una función por partes depende de su definición. En el ejemplo anterior, el dominio es el conjunto formado por: (–∞,-1) ∪ [1,+∞).

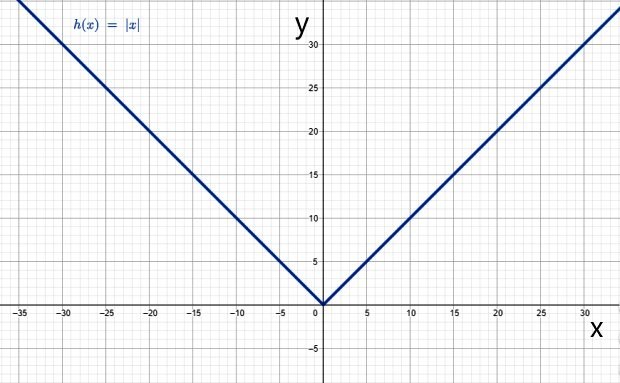
i) Función valor absoluto
La siguiente función a trozos se conoce como función valor absoluto:
A diferencia de la función identidad, esta función tiene como salida al mismo número de la entrada, pero con signo positivo y el dominio son todos los reales.
ii) Función escalonada
La gráfica de esta función por tramos consiste en peldaños, como los de una escalera o bien pueden ser de diferentes alturas, según la forma en que se defina la función.
Para ello se elige un intervalo finito [a,b] que contenga un cierto número finito de discontinuidades, llamadas xi < x1 < x2 <…. xn y se elige un intervalo abierto (xi , xi+1) para darle un constante de valor si, con los saltos en los puntos xi. El valor de si es la altura del peldaño en cuestión.
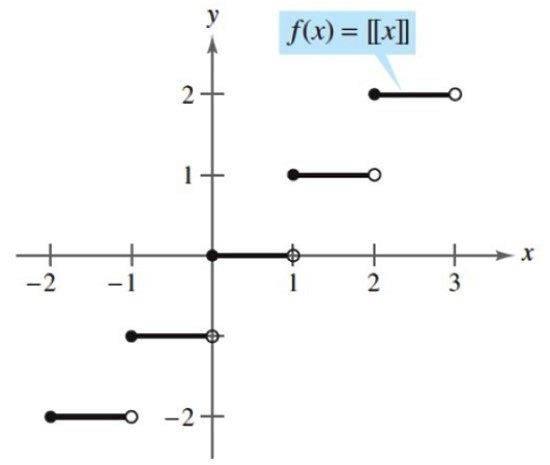
Un ejemplo de función escalonada es la función parte entera, que toma un número cualquiera y lo asocia con el entero siguiente, ya sea por exceso o por defecto. La siguiente es una función parte entera:
[x] = (mayor entero ≤ x)
Según esta función, la parte entera de 2.5 es:
[2.5] = (mayor entero ≤ 2.5) = 2
I.2) Funciones trascendentes
Las funciones no algebraicas se denominan trascendentes. Las funciones exponenciales, logarítmicas y trigonométricas son funciones trascendentes.
En ellas la variable x forma parte del argumento de la función o como parte del exponente o el índice de alguna raíz, por ejemplo:
- f(x) = log (x+1)
- h(x) = -0.2⋅8-3x
Las funciones trascendentes tienen muchas aplicaciones, por ejemplo en el estudio de vibraciones y ondas, las distribuciones de probabilidad, modelado de las olas del mar, el crecimiento de poblaciones diversas, el decaimiento radiactivo, las tasas de interés y muchas más.
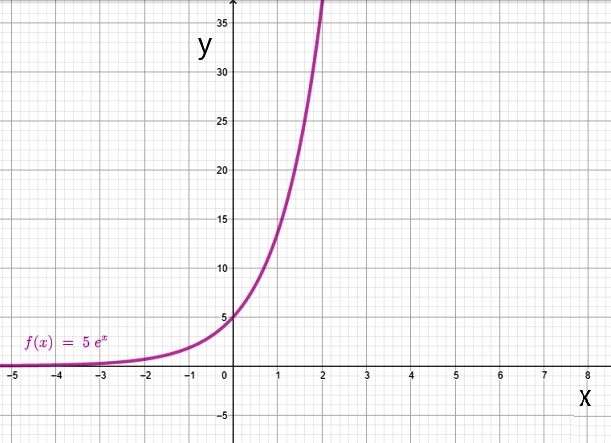
I.2.a) Función exponencial
La función exponencial se define mediante:
f(x) = ax
Donde a es la base, que siempre es un número positivo diferente de 1, y la variable, un número real, aparece en el exponente. En forma general, la función exponencial se escribe:
f(x) = A⋅aBx
Aquí A y B son coeficientes reales. Las siguientes son funciones de este tipo:
- f(x) = 5ex
- h(x) = 4. 105x
- g(t) = 8e-2t
La base e, donde e es el número de Euler 2.71828…, aparece frecuentemente en problemas de ciencia e ingeniería, así como en estadística. Cuando la función tiene esta base se denomina función exponencial natural.
El dominio de la función exponencial es el conjunto de los números reales, mientras que el rango son los números reales positivos.
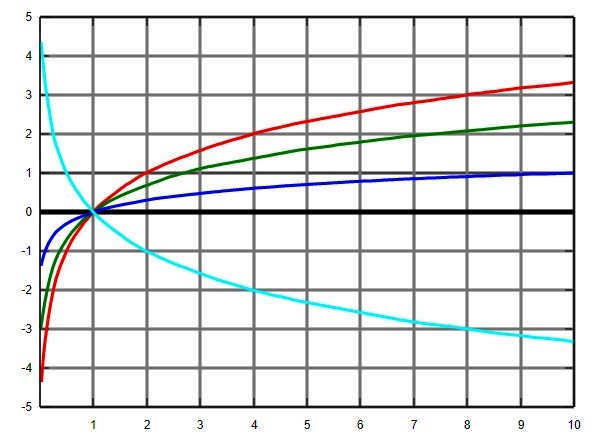
I.2.b) Función logaritmo
Por su parte, la función logaritmo en base a es la función inversa de la función exponencial en base a. Si:
loga x = y
Entonces:
x = ay
En particular, si la base del logaritmo es el número e, la función se denomina función logaritmo neperiano y se denota como ln. Funciones de este tipo son:
- f(x) = ln x
- g(x) = log (x+1)
- h(t) = 1 – log x2
El dominio de la función logaritmo, sin importar la base, son los números reales positivos, sin incluir al 0. Es decir, no existen logaritmos de números negativos ni de 0.
Sin embargo, un logaritmo sí puede ser 0 o negativo: el logaritmo del número comprendido entre 0 y 1 es negativo y por su parte loga 1 = 0.
I.2.c) Funciones trigonométricas
Son las que provienen de las razones trigonométricas: seno, coseno, tangente, secante, cosecante y cotangente de un ángulo dado x. Se denotan respectivamente como:
sen x, cos x, tg x, sec x, cosec x y cotg x
Son funciones periódicas, lo que significa que su forma es repetitiva, por ello son muy útiles para describir fenómenos naturales tales como señales, oscilaciones, movimiento circular y movimientos de vaivén, que se caracterizan por ser repetitivos.
Ejemplos de funciones trigonométricas son:
- f(x) = sen x
- g(t) = 5⋅cos (ωt + π)
- h(x) = tg (x/2)
La variable x se expresa en radianes.
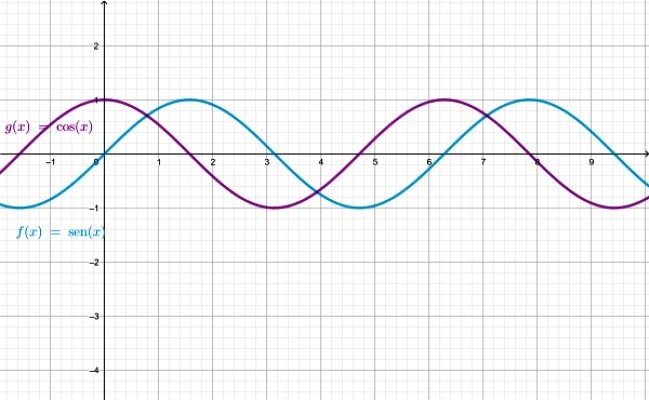
El dominio de las funciones sen x y cos x, es el conjunto de los números reales. Para las restantes funciones hay valores de x para los cuales la función no está definida:
-La función tg x no existe cuando x = ±π /2, ±5π /2… esto es, todos los múltiplos impares de π /2.
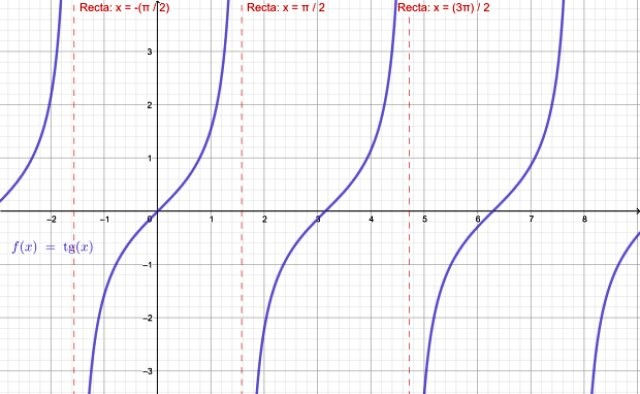
-En cuanto a f(x) =cotg x, esta función no está definida para los múltiplos enteros de π: ±π, ±2π, ±3π…
-La función y = sec x no es válida cuando cos x = 0, lo que excluye a x = ±π /2, ±5π /2… de su dominio.
-Por último, para f(x) = cosec x, los múltiplos enteros de π no pertenecen a su dominio.
I.2.d) Funciones hiperbólicas
Las funciones hiperbólicas son combinaciones especiales de exponenciales ex y e-x y se denominan como seno, coseno….hiperbólico. Al igual que con las funciones trigonométricas, también llamadas “circulares”, hay 6 funciones hiperbólicas:
–Seno hiperbólico senh x:
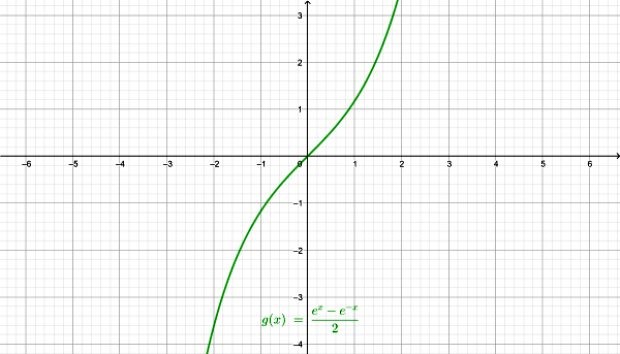
–Coseno hiperbólico cosh x:
–Tangente hiperbólica tanh x:
–Cosecante hiperbólica csch x:
–Secante hiperbólica sech x:
–Cotangente hiperbólica coth x:
Un cable flexible, hecho de material uniforme y colgado entre dos puntos, toma la forma de una curva llamada catenaria, la cual se expresa como un coseno hiperbólico:
I.2.e) Funciones trigonométricas inversas
Corresponden a las inversas de las funciones trigonométricas. Por ejemplo, ¿cuál sería el ángulo (arco) cuyo seno vale 0.5?
La respuesta es el arc sen 0.5, que se lee “arco seno de 0.5”, y este ángulo es 30º, aunque en principio, este no sería el único ángulo cuyo seno vale 0.5, puesto que la función sen x es periódica. Lo que sucede es que si se toma la función sen x en todo su dominio, no tendría inversa, por lo que no podría definirse la función arcoseno. La cuestión queda zanjada restringiendo todo a los ángulos comprendidos entre -π/2 y +π/2.
Esto se puede expresar así:
Si arc sen x = θ, quiere decir que sen θ = x
Con -π/2 ≤ θ ≤ π/2.
Otra notación usada con frecuencia para el arc sen x es f(x) = sen-1 x. La gráfica se muestra a continuación:
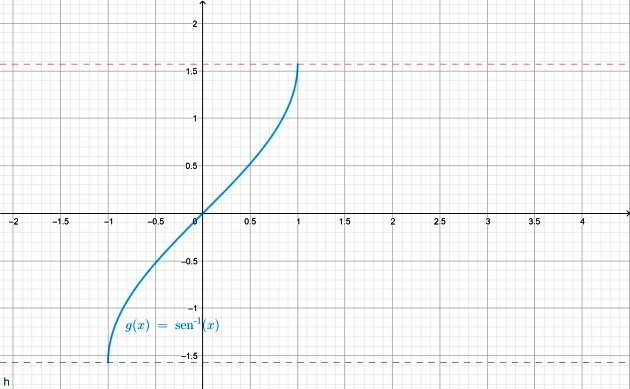
También es posible definir inversas para las demás funciones trigonométricas, por ejemplo: arc cos x = θ y así. Para cada una se restringe el rango adecuadamente, para que sea la inversa de la correspondiente función trigonométrica.
II) Funciones según su simetría
II.1) Función par
Si para todo x perteneciente al dominio de f(x) se cumple que:
f(x) = f(-x)
Se dice que la función es par, como las que siguen:
- f(x) = x2 – 3
- g(x) = cos x
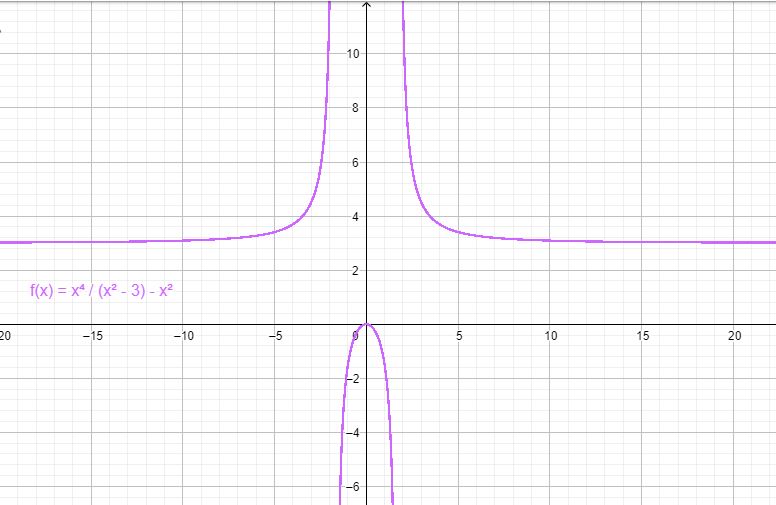
Ejemplo de una función par. Fuente: F. Zapata a través de Geogebra.
Por ejemplo, haciendo x = 1 en f(x) = x2 – 3 se obtiene:
f(1) = 12 – 3 = -2.
Y si se hace x = -1, entonces:
f(-1) = (-1)2 – 3 = -2.
Ambos resultados son idénticos.
Las funciones pares tienen simetría alrededor del eje vertical, como se aprecia en la figura anterior.
II.2) Función impar
Por otro lado, si:
f(-x) = -f(x)
La función es impar.
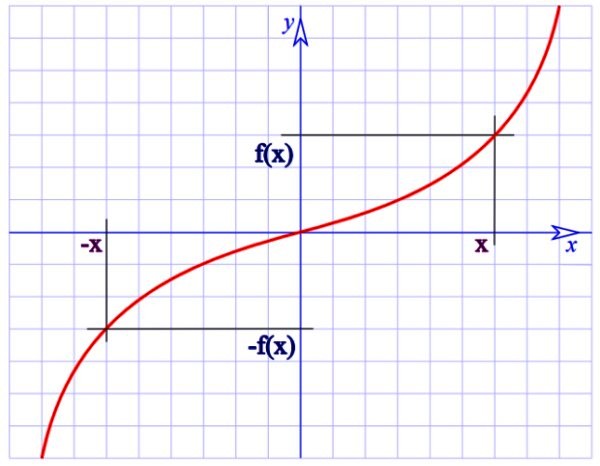
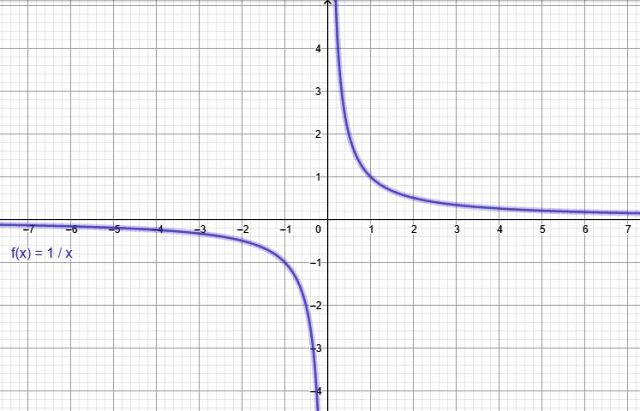
Por ejemplo la función f (x)= 1/x de la figura superior es impar, ya que:
f(-x) = -1/x
Y
-f (x) = -1/x
Otra importante función impar es f(x) = sen x.
Nótese que las funciones impares tienen simetría de rotación de 180º alrededor del origen (la gráfica no se altera si cada punto de la misma se gira 180º respecto al origen de coordenadas).
III) Función según la expresión de la variable
III.1) Funciones explícitas
Se expresan directamente en términos de la variable dependiente como y = f(x). Por ejemplo:
- f(x) = x3
III.2) Funciones implícitas
En las funciones implícitas ninguna de las variables aparece despejada. Se expresan como F(x,y) =0, tales como:
- x2 + y2 -3xy = 0
- xy= – x2+ x-5
Las funciones descritas a lo largo de este artículo son funciones explícitas.
IV) Funciones según su gráfica
De acuerdo a su gráfica, las funciones pueden ser continuas o discontinuas. Las funciones continuas se pueden trazar sin necesidad de interrumpir el trazo, en cambio, las funciones discontinuas presentan saltos. En la siguiente imagen, la función es discontinua en x = a:
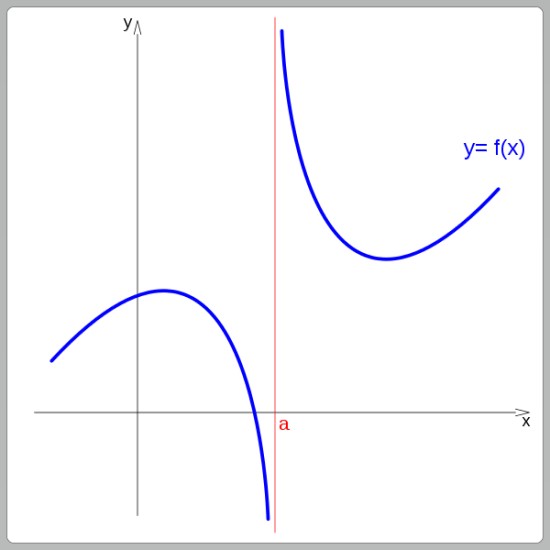
Ejemplos de funciones continuas son la función lineal, la función cuadráticas y las funciones seno y coseno. Y entre las funciones discontinuas son la función escalonada y la función tangente.
V) Funciones según la relación entre los elementos del dominio y el rango
V.1) Función inyectiva
Una función es inyectiva cuando no hay dos elementos distintos en el conjunto de partida o dominio, que tengan la misma imagen en el conjunto de llegada.
Supóngase que se tienen funciones reales, a menos que se especifique otra cosa, por ejemplo:
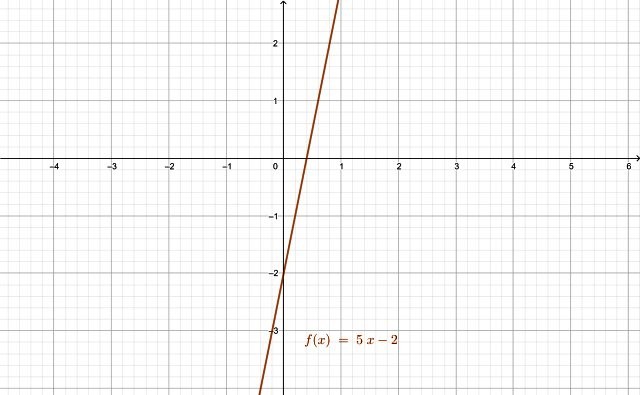
f(x) = 5x -2
Todo valor de x perteneciente al dominio de f(x), que es el conjunto ℛ de los números reales, tiene una imagen única, también real. En cambio, en esta otra función:
g(x) = x2
Hay elementos diferentes en el dominio que tienen la misma imagen, por ejemplo x1= 2 y x2= -2:
g(2) = g(-2) = 4.
La forma de identificar una función inyectiva a partir de su gráfica es trazando una recta horizontal, si esta corta a la curva en más de un punto, la función es no inyectiva.
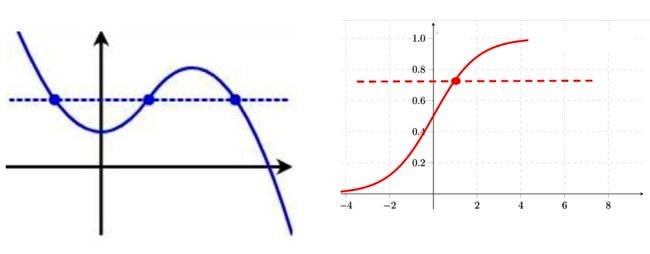
V.2) Función sobreyectiva
En las funciones sobreyectivas, todos los elementos del conjunto de llegada son imagen de algún elemento del conjunto de partida. Un ejemplo de función sobreyectiva es la misma f(x) = 5x -2, pero g(x) = x2 no lo es, puesto que los valores que toma g(x) son únicamente los reales positivos y el 0.
Sin embargo, el dominio pudiera redefinirse para que g(x) fuera sobreyectiva, si por ejemplo se cambia a todos los reales positivos más el 0.
V.3) Función biyectiva
Por último, una función que sea a la vez inyectiva y sobreyectiva, se denomina biyectiva. Ejemplos de funciones biyectivas son: la función afín, la función exponencial y la función logaritmo.


.jpg)
Comentarios
Publicar un comentario